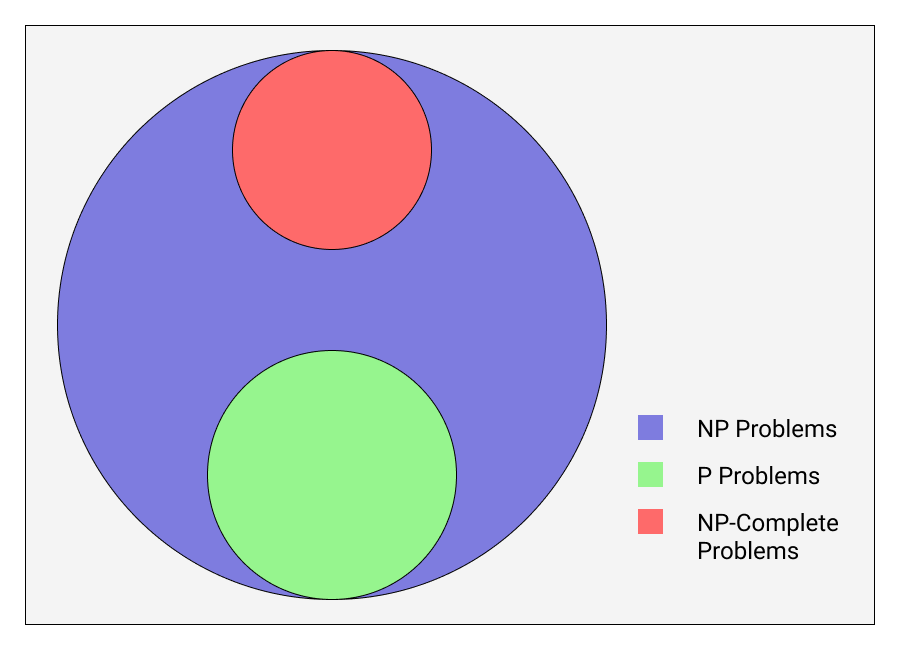
The above image represents something completely un-understandable to me during my college years. I couldn't understand what the professor tried to explain during my algorithms class when the topic of P vs NP vs NP-Complete problems came.

Finally I understood it from a video by "Up and Atom". The problems are grouped according to these 2 criteria:

1. Can a solution to the problem be found in polynomial time?

2. Can a given solution for the problem be verified in polynomial time?

NP Problems

These are the problems for which condition 2 holds true. If given a solution to such problem, the correctness of that solution can be verified in polynomial time. Condition 1 being true or false for such problems doesn't affect whether they can fall under NP category or not.

NP-Complete Problems

These are the problems for which condition 2 holds true but condition 1 is false. A valid solution to the problem can't be verified in polynomial time, but if given a solution to the problem the correctness of that solution can be verified in polynomial time.

P Problems

For these problems, both conditions 1 & 2 hold true. There exist methods by which a valid solution to any of these problem can be found under polynomial time. And also, any given solution for such problem can be verified in polynomial time.

Want to discuss this or any other interesting thing, hit me up on Twitter @varun_barad.